AutoLISP tutorial: Working with layers

An AutoLISP program doesn’t have to be difficult. We can create simple LISP program and get many benefits from it. It’s not just about speed up the drawing creation, but also to maintain our standard.

In system variable and COND conditional, we discussed how we can use block to create grids. This will ensure the users (or you) to use the same block for every drawing. Now let’s see how to control the other properties you need to control: layers and styles. Let’s explore the possibility to use it to control our drawing standard.

Working with layers

Layers are the most important thing to manage our drawings. If you’re not familiar with layer standard, CADD manager has a short article about the concept.

Changing the current layer

We can change the current layer using setvar. We did it before here. Current layer variable is controlled by CLAYER.

(setvar "CLAYER" "LAYERNAME")

Sample: creating text

Now let’s try an example. We want to create a LISP program to create text, and use a default layer. This is what we do:

1. Get current layer and save it to a variable.
2. Set current layer to a different layer. In this sample, annotation layer.
3. We ask for required data for creating text. In this sample we ask for text content and position. You may want to consider ask for height and rotation angle. But it’s not necessary in this sample.
4. Set the current layer to previous layer.

This is the code after we put it all together:

(defun c:cntext ()
(setq oldlayer (getvar "CLAYER")) ; get current layer
(setvar "CLAYER" "A-Anno")        ; change layer to annotation layer
(setq textcontent (getstring "
Type Text: "))
(setq textloc (getpoint "
Text Position: "))
(command "_TEXT" textloc "" "" textcontent) ;create the text
(setvar "CLAYER" oldlayer) ;restore active layer
)

Check for existing layer

It should works. But we still have a problem. What if the layer doesn’t exist? AutoCAD returns error warning.

; error: AutoCAD variable setting rejected: “clayer” “layername”

We need to check if the layer exist or not first. We can do it by using this code:

(setq flag (tblsearch "LAYER" "A-Anno"))

Then add conditional IF like this:

(if flag

(PUT WHAT YOU WANT AUTOCAD TO DO HERE)

(ELSE DO THIS)

)

We have discussed about using conditional IF in AutoLISP before. The problem is IF only allows you to run one statement. So we need to add (progn GROUP OF STATEMENTS) to run several statements.

Let’s see the complete code below:

(defun c:cntext ()
(setq flag (tblsearch "LAYER" "A-Anno")) ;looking for A-Anno layer
;then do this if exist
(if flag
(progn ;grouping statement
(setq oldlayer (getvar "CLAYER"))
(setvar "CLAYER" "A-Anno")
(setq textcontent (getstring "
Type Text: "))
(setq textloc (getpoint "
Text Position: "))
(command "_TEXT" textloc "" "" textcontent)
(setvar "CLAYER" oldlayer)
) ;end statement group
;else - and give warning if it doesn't exist
(alert "No A-Anno layer. Create it first to maintain standard.")
) ; end if
)

Now AutoCAD will try to find the layer first before executing our command. If it doesn’t exist, then it will give a warning.

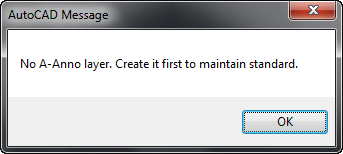
If the layer exists, then it will run our program.

There are several possibilities to handle this situation. We will see in the next tutorial, other alternatives to deal with non-exist layers.

credit: this article was written based on this AfraLISP tutorial.

About Edwin Prakoso

I work as a Solution Consultant in Datech Solutions, Tech Data Indonesia. I've been using AutoCAD since R14 and Revit since Revit Building 9. I occasionally write for AUGIWorld magazine and I am also active in Autodesk discussion forum. I'm a member of Autodesk Expert Elite, an appreciation for individuals who give contributions to the Autodesk community.
Connect with me on twitter or LinkedIn.